Java Towers of Hanoi Recursion Visualization Towers Easy

Program for Tower of Hanoi

View Discussion

Improve Article

Save Article

Like Article

Tower of Hanoi is a mathematical puzzle where we have three rods and n disks. The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:

1. Only one disk can be moved at a time.
2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack i.e. a disk can only be moved if it is the uppermost disk on a stack.
3. No disk may be placed on top of a smaller disk.

Approach :

Let rod 1 = 'A', rod 2 = 'B', rod 3 = 'C'. An example with              2 disks              : Step 1 : Shift first disk from 'A' to 'B'.  Step 2 : Shift second disk from 'A' to 'C'.  Step 3 : Shift first disk from 'B' to 'C'.

An example with              3 disks              : Step 1 : Shift first disk from 'A' to 'C'. Step 2 : Shift second disk from 'A' to 'B'. Step 3 : Shift first disk from 'C' to 'B'.  Step 4 : Shift third disk from 'A' to 'C'.  Step 5 : Shift first disk from 'B' to 'A'. Step 6 : Shift second disk from 'B' to 'C'. Step 7 : Shift first disk from 'A' to 'C'.              (Notice the gaps)            

The pattern here is :  - Shift 'n-1' disks from 'A' to 'B', using C.  - Shift last disk from 'A' to 'C'.  - Shift 'n-1' disks from 'B' to 'C', using A.

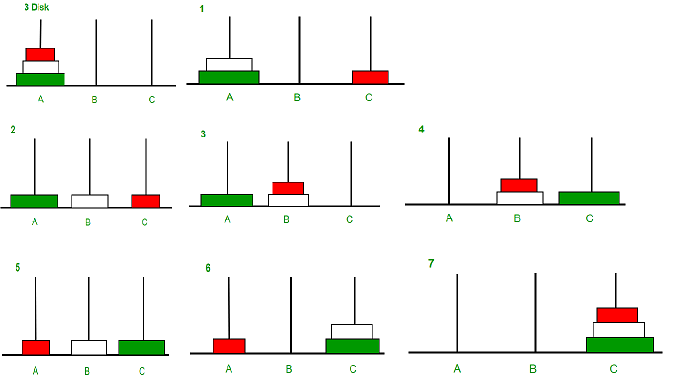
Image illustration for 3 disks

Examples:

Input : 2 Output : Disk 1 moved from A to B          Disk 2 moved from A to C          Disk 1 moved from B to C  Input : 3 Output : Disk 1 moved from A to C          Disk 2 moved from A to B          Disk 1 moved from C to B          Disk 3 moved from A to C          Disk 1 moved from B to A          Disk 2 moved from B to C          Disk 1 moved from A to C

Implementation:

C++

#include <bits/stdc++.h>

using namespace std;

void towerOfHanoi( int n, char from_rod,

char to_rod, char aux_rod)

{

if (n == 0)

{

return ;

}

towerOfHanoi(n - 1, from_rod, aux_rod, to_rod);

cout << "Move disk " << n << " from rod " << from_rod <<

" to rod " << to_rod << endl;

towerOfHanoi(n - 1, aux_rod, to_rod, from_rod);

}

int main()

{

int n = 4;

towerOfHanoi(n, 'A' , 'C' , 'B' );

return 0;

}

Java

import java.util.*;

import java.io.*;

import java.math.*;

class GFG

{

static void towerOfHanoi( int n, char from_rod,

char to_rod, char aux_rod)

{

if (n == 0 )

{

return ;

}

towerOfHanoi(n - 1 , from_rod, aux_rod, to_rod);

System.out.println( "Move disk " + n + " from rod " +

from_rod + " to rod " + to_rod );

towerOfHanoi(n - 1 , aux_rod, to_rod, from_rod);

}

public static void main(String args[])

{

int n = 4 ;

towerOfHanoi(n, 'A' , 'C' , 'B' );

}

}

Python3

def TowerOfHanoi(n , from_rod, to_rod, aux_rod):

if n = = 0 :

return

TowerOfHanoi(n - 1 , from_rod, aux_rod, to_rod)

print ( "Move disk" ,n, "from rod" ,from_rod, "to rod" ,to_rod)

TowerOfHanoi(n - 1 , aux_rod, to_rod, from_rod)

n = 4

TowerOfHanoi(n, 'A' , 'C' , 'B' )

C#

using System;

class GFG

{

static void towerOfHanoi( int n, char from_rod, char to_rod, char aux_rod)

{

if (n == 0)

{

return ;

}

towerOfHanoi(n-1, from_rod, aux_rod, to_rod);

Console.WriteLine( "Move disk " + n + " from rod " +

from_rod + " to rod " + to_rod);

towerOfHanoi(n-1, aux_rod, to_rod, from_rod);

}

public static void Main(String []args)

{

int n = 4;

towerOfHanoi(n, 'A' , 'C' , 'B' );

}

}

PHP

<?php

$poles = array ( array (), array (), array ());

function TOH( $n , $A = "A" , $B = "B" , $C = "C" ){

if ( $n > 0){

TOH( $n -1, $A , $C , $B );

echo "Move disk from rod $A to rod $C \n" ;

move( $A , $C );

dispPoles();

TOH( $n -1, $B , $A , $C );

}

else {

return ;

}

}

function initPoles( $n ){

global $poles ;

for ( $i = $n ; $i >=1; -- $i ){

$poles [0][] = $i ;

}

}

function move( $source , $destination ){

global $poles ;

if ( $source == "A" ) $ptr1 =0;

elseif ( $source == "B" ) $ptr1 = 1;

else $ptr1 = 2;

if ( $destination == "A" ) $ptr2 = 0;

elseif ( $destination == "B" ) $ptr2 = 1;

else $ptr2 = 2;

$top = array_pop ( $poles [ $ptr1 ]);

array_push ( $poles [ $ptr2 ], $top );

}

function dispPoles(){

global $poles ;

echo "A: [" .implode( ", " , $poles [0]). "] " ;

echo "B: [" .implode( ", " , $poles [1]). "] " ;

echo "C: [" .implode( ", " , $poles [2]). "] " ;

echo "\n\n" ;

}

$numdisks = 4;

initPoles( $numdisks );

echo "Tower of Hanoi Solution for $numdisks disks: \n\n" ;

dispPoles();

TOH( $numdisks );

?>

Javascript

<script>

function towerOfHanoi(n, from_rod,  to_rod,  aux_rod)

{

if (n == 0)

{

return ;

}

towerOfHanoi(n - 1, from_rod, aux_rod, to_rod);

document.write( "Move disk " + n + " from rod " + from_rod +

" to rod " + to_rod+ "<br/>" );

towerOfHanoi(n - 1, aux_rod, to_rod, from_rod);

}

var n = 4;

towerOfHanoi(n, 'A' , 'C' , 'B' );

</script>

Output

Move disk 1 from rod A to rod B Move disk 2 from rod A to rod C Move disk 1 from rod B to rod C Move disk 3 from rod A to rod B Move disk 1 from rod C to rod A Move disk 2 from rod C to rod B Move disk 1 from rod A to rod B Move disk 4 from rod A to rod C Move disk 1 from rod B to rod C Move disk 2 from rod B to rod A Move disk 1 from rod C to rod A Move disk 3 from rod B to rod C Move disk 1 from rod A to rod B Move disk 2 from rod A to rod C Move disk 1 from rod B to rod C

Time complexity: O(2^n)
Space complexity: O(n)

Related Articles

• Recursive Functions
• Iterative solution to TOH puzzle
• Quiz on Recursion

stonerhatteniou1990.blogspot.com

Source: https://www.geeksforgeeks.org/c-program-for-tower-of-hanoi/

Share this post